?

1.SGD

2.BGD

3.MBGD：

.批量梯度下降：每次更新使用了所有的训练数据，最小化损失函数，如果只有一个极小值，那么批量梯度下降是考虑了训练集所有的数据，是朝着最小值迭代运动的，但是缺点是如果样本值很大的话，更新速度会很慢。
.随机梯度下降：在每次更新的时候，只考虑一个样本点，这样会大大加快训练数据，也恰好是批量梯度下降的缺点，但是有可能由于训练数据的噪声点较多，那么每一次利用噪声点进行更新的过程中，就不一定是朝着极小值方向更新，但是由于更新多轮，整体方向还是朝着极小值方向更新，又提高了速度。
.小批量梯度下降法：是二者折中的算法。是为了解决批量梯度下降的训练速度慢，以及随机梯度下降法的准确性综合而来，但是这里注意，不同问题的batch是不一样的，要通过实验结果来进行超参数的调

4.动量：要是当前时刻的梯度与历史时刻梯度方向相似，这种趋势在当前时刻则会加强；要是不同，则当前时刻的梯度方向减弱

?

?

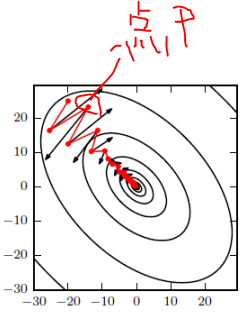
SGD 在 ravines 的情况下容易被困住， ravines 就是曲面的一个方向比另一个方向更陡，这时 SGD 会发生震荡而迟迟不能接近极小值：

?

5.

RMSprop 是 Geoff Hinton 提出的一种自适应学习率方法。

RMSprop 和 Adadelta 都是为了解决 Adagrad 学习率急剧下降问题的，

梯度更新规则:

RMSprop 与 Adadelta 的第一种形式相同：（使用的是指数加权平均，旨在消除梯度下降中的摆动，与Momentum的效果一样，某一维度的导数比较大，则指数加权平均就大，某一维度的导数比较小，则其指数加权平均就小，这样就保证了各维度导数都在一个量级，进而减少了摆动。允许使用一个更大的学习率η）

?

超参数设定值:

Hinton 建议设定 γ 为 0.9, 学习率 η 为 0.001。

6.

这个算法是另一种计算每个参数的自适应学习率的方法。相当于 RMSprop + Momentum

除了像 Adadelta 和 RMSprop 一样存储了过去梯度的平方 vt 的指数衰减平均值 ，也像 momentum 一样保持了过去梯度 mt 的指数衰减平均值：

如果 mt 和 vt 被初始化为 0 向量，那它们就会向 0 偏置，所以做了偏差校正，通过计算偏差校正后的 mt 和 vt 来抵消这些偏差：

梯度更新规则:

超参数设定值:
建议 β1 ＝ 0.9，β2 ＝ 0.999，? ＝ 10e?8

实践表明，Adam 比其他适应性学习方法效果要好。

?